
Inicjalizacja danych klasyfikacyjnych
Inicjalizacja danych wieloparametrowych, poddawanych klasyfikacji, jest podobna do tej z rozdziału 4.2 , lecz nie identyczna. Dane poddawane klasyfikacji posiadają wiele parametrów, które należy pojedynczo normalizować/standaryzować.
Wybór zmiennych objaśniających
Nieraz spotykamy się z danymi klasyfikacyjnymi, które posiadają bardzo dużą ilość zmiennych objaśniających (parametrów). Kiedy próbujemy stworzyć dla nich model danych np. za pomocą Sieci Neuronowych, lub takich algorytmów jak K-Najbliższych Sąsiadów lub podobnych, zdarza się, że wyniki testów klasyfikacyjnych są dla nas nieoczekiwanie złe. Często jest to związane z wysokim skorelowaniem statystyk, co prowadzi nader często do niestabilności modelu klasyfikacyjnego. Dodatkowo mnogość parametrów sprowadza się do zwiększenia czasu oczekiwania na rezultaty klasyfikacji. Wówczas najlepszym wyjściem jest usunięcie zbędnych parametrów, dzięki czemu pozbywamy się korelacji pomiędzy parametrami, oraz optymalizujemy czas klasyfikacji.
Istnieje wiele metod redukcji wymiaru macierzy wejściowej. Do najczęściej stosowanych zalicza się:
- usuwanie zbędnych parametrów, mających wysoki współczynnik wzajemnej korelacji,
- komponenty zdefiniowane przez użytkownika,
- analiza składowych głównych (PCA),
- analiza czynnikowa,
- wybór najlepszej kombinacji za pomocą algorytmów genetycznych.
W niniejszym rozdziale, przedstawiono inny sposób analizy parametrów, zaczerpnięty z [8], a szerzej opisany w [7, 22, 21].
Warunki ogólne
Warunkiem podstawowym do optymalnego wyboru statystyk, jest dobra znajomość zagadnienia jakie będziemy modelować. Dzięki wiedzy dotyczącej danego zagadnienia, możemy wstępnie wytypować wielkości mające wpływ na zachowanie wyjścia modelu. Po wstępnym ustaleniu zmiennych modelu, celem redukcji nadmiarowości statystyk należy przyjąć założenie, że wyjście (np. klasa) jest liniowo powiązana ze zmiennymi objaśniającymi. W przeciwnym wypadku gdy z jakiegoś powodu nie możemy przyjąć powyższego założenia, przedstawiony sposób nie będzie optymalny.
W pierwszej kolejności należy odpowiednio zgrupować dane w macierz pomiarów M.
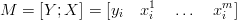 | (4.1) |
gdzie:
m jest liczbą zmiennych objaśniających,
i = 1, 2,...n oznacza kolejne realizacje zmiennych.
Liczba realizacji n, powinna być znacznie większa od liczby zmiennych objaśniających m [8].
Celem uniknięcia niejednoznaczności sformułowań, wprowadzone zostaną następujące pojęcia:
- nośnik informacji nazywa się zmienną objaśniającą,
- pojemnością indywidualną nośnika informacji nazywa się wyrażenie,
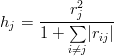
(4.2)
gdzie:
hj - jest pojemnością indywidualną j-tej zmiennej objaśniającej,
rj - jest współczynnikiem korelacji j-tej zmiennej objaśniającej z wyjściem,
rij - jest współczynnikiem korelacji i-tej i j-tej zmiennej objaśniającej.
- pojemnością integralną nośników informacji nazywamy sumę pojemności indywidualnych,
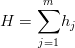
(4.3)
Celem zoptymalizowania zmiennych objaśniających niniejszą metodą jest takie wybranie kombinacji zmiennych objaśniających tak, aby pojemność integralna była największa. W pracy nieznacznie zmodyfikowano to założenie, gdyż uważa się, że w pewnych wypadkach pojemność integralna danej kombinacji obrazuje zbyt małą część modelu, tak więc można wówczas wybrać N kombinacji statystyk których pojemność integralna jest najwyższa. Dzięki temu przy bardzo dużej ilości zmiennych, można zoptymalizować model danych równocześnie uwzględniając większą część właściwości danego modelu.
Przykład redukcji statystyk
Przyjmijmy następującą macierz wejściową M,
 | (4.4) |
Przyjmijmy teraz następujące założenia:
- Współczynnik korelacji zmiennej wyjściowej, ze zmiennymi objaśniającymi,
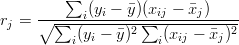
(4.5)
gdzie: i=1,...,5; j=1,2,3.
Dla rozpatrywanego przykładu korelacje parametrów ze zmienną wyjściową wynoszą odpowiednio: r1 = 0.1686, r2 = 0.0515, r3 = 0.7403.
- Współczynnik korelacji wzajemnej zmiennych objaśniających,
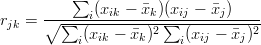
(4.6)
Zauważmy, że liczba możliwych kombinacji zmiennych objaśniających wraz ze wzrostem parametrów modelu wzrasta wykładniczo. Ilość kombinacji obliczamy według wzoru K = (2n - 1), co w naszym wypadku K = 28 - 1 = 7.
Tablica 4.1: Kombinacje zmiennych objaśniających
| Nr | Kombinacja | Binarnie |
| K1 | x1 | 001 |
| K2 | x2 | 010 |
| K3 | x1,x2 | 011 |
| K4 | x3 | 100 |
| K5 | x1,x3 | 101 |
| K6 | x2,x3 | 110 |
| K7 | x1,x2,x3 | 111 |
Źródło: Badania własne
Tabela 4.1 przedstawia sposób, jaki można zaimplementować do maszynowego wyznaczania kombinacji zmiennych objaśniających. Sposób ten, jest o tyle efektywny dlatego, że opiera się na systemie dwójkowym. Odpowiednie zestawienie bitów tworzy kombinacje zmiennych objaśniających.
Dla poszczególnych kombinacji zmiennych objaśniających obliczono indywidualne pojemności nośników hkj (k - numer kombinacji, j -numer zmiennej):
h11 = r12 = 0.0284;
h22 = r22 = 0.0026;
h31 = 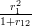 = 0.0253; h32 =
= 0.0253; h32 = 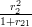 = 0.0023;
= 0.0023;
h43 = r32 = 0.5481;
h51 =  = 0.0271; h53 =
= 0.0271; h53 = 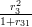 = 0.5231;
= 0.5231;
h62 =  = 0.0020; h63 =
= 0.0020; h63 = 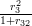 = 0.4071;
= 0.4071;
h71 = 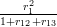 = 0.0243; h72 =
= 0.0243; h72 =  = 0.0018; h73 =
= 0.0018; h73 = 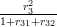 = 0.3932;
= 0.3932;
Pojemności integralne dla każdej kombinacji wynoszą odpowiednio:
H1 = h11 = 0.0284
H2 = h22 = 0.0026
H3 = h31 + h32 = 0.0276
H4 = h43 = 0.5481
H5 = h51 + h53 = 0.5502
H6 = h62 + h63 = 0.4091
H7 = h71 + h72 + h73 = 0.4193
Jak widzimy, najlepszą kombinacją statystyk jest kombinacja K5 dlatego, że posiada największą pojemność integralną informacji.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.