
Metoda składania prognoz jednokrokowych
Jak już wcześniej zostało wspomniane, algorytmy 8.1 nie umożliwiają dokonania prognozy która obejmowała by okres większy niż okres segmentu danych. Istnieje jednak sposób na ominięcie tej niedogodności. Tym sposobem jest metoda predykcji prognoz jednokrokowych oraz ich składanie. Jak już można się domyślać, jest to logiczne rozwinięcie metody predykcji z poprzedniego rozdziału z tą różnicą, że predykcja ta umożliwia obejście bariery okna czasowego.
Prognozę wielokrokową w przedziale (1,k) ciągu czasowego można złożyć z k prognoz jednokrokowych punktowych, wyliczanych według jednokrokowego algorytmu predykcji [8].
Algorytm 9.1: Jednokrokowa predykcja składana.
Wykonuj predykcję N razy
- Dla każdej iteracji, oblicz predykcję dla wektora Input, z zakresu iter : iter + m - 2
- Wywołaj funkcję addPoint, która:
- zdenormalizuje odpowiedź
- obliczy wartość odpowiedzi w kontekście wektora wejściowego Input
- doda znormalizowaną odpowiedź do wektora Input
- Inkrementuj licznik iter
- Input
- - wektor wejściowy
- N
- - docelowy horyzont predykcji
- iter
- - licznik kroków predykcji
- m
- - długość wektora Input
Krótko mówiąc algorytm wykonuje normalną predykcję z tym, że predygujemy z horyzontem predykcji = 1. Następnie pomijając pierwszy element wektora wyjściowego umieszczamy na wejście algorytmu, poprzednio zwrócony wektor.
Rysunek 9.1: Predykcja n-dniowa, długoterminowa.
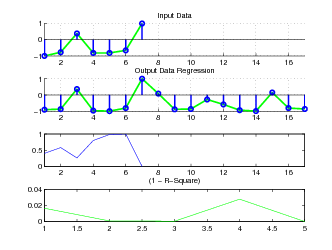
Źródło: Badania własne.
Zalety tak skonstruowanego predyktora są następujące:
- predyktor wielokrokowy składany wykorzystuje wszelkie dostępne informacje o ciągu, prognozach i błędach predykcji,
- prognoza wielokrokowa jest obarczana błędem, wynikającym ze sumowania błędów jednokrokowych punktowych predykcji.
Do wad można zaliczyć to, że obliczenie takiej predykcji potrzebuje wielu iteracji, a co się z tym wiąże, czas predykcji jest zdecydowanie dłuższy niż predykcji opisanej w rozdziale 8 . Należy pamiętać, że czym większy horyzont predykcji, tym większa staje się niepewność prognozy [8].
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.