
Przykładowe użycie klasyfikatora DNA
Przykład przeprowadzono na jednej iteracji algorytmu, a dane przykładowe pochodzą z [1]. Poniżej przedstawione są parametry wejściowe algorytmu:
Rysunek 6.2: Dyskretyzacja danych wejściowych
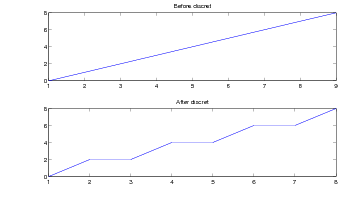
Źródło: Badania własne
- input - macierz wejściowa (tabela 5.1 )
- mindist = 0.1
- maxdist = 0.15
- maxpula = 5
- N = 256
- pmut = 0.01
- rmut = 0.05
- pcross = 0.4
- mincorel = 0.98
Poszczególne parametry mają następujące znaczenia:
- mindist
- - minimalna różnica pomiędzy chromosomami,
- maxdist
- - maksymalna różnica pomiędzy chromosomami,
- maxpula
- - maksymalna pula chromosomów, z których losowane będą chromosomy poddawane operacji cross-over i mutacji,
- N
- - ilość przedziałów dla dyskretyzacji,
- pmut
- - prawdopodobieństwo mutacji, zazwyczaj bardzo małe,
- rmut
- - "promień mutacji", czyli maksymalny promień od punktu mutowanego,
- pcross
- - prawdopodobieństwo przeprowadzenia krzyżowania (cross-over),
- mincorel
- - minimalny współczynnik korelacji (dopasowania).
Poniżej przedstawione jest wywołanie funkcji classDNA w środowisku Matlab:
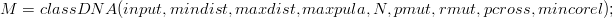
W funkcji classDNA wyszukiwany jest najbardziej odpowiedni chromosom dla każdego wektora, przy każdej iteracji do zmiennej ch (tabela 6.1 ) przypisywany jest i - ty wektor macierzy wejściowej.
Tablica 6.1: Wektor ch
| 1,170020243 | 0,435889894 | -0,527656188 | -1,078253949 |
Źródło: Badania własne
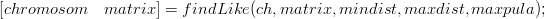
Funkcja zwraca losowy chromosom, z puli maxpula najlepiej dopasowanych chromosomów (tabela 6.2 ).
Tablica 6.2: Chromosom odpowiedzi
| 1,19324 | 0,361928 | -0,460348 | -1,11094 |
Źródło: Badania własne
Kolejny krok realizowany przez algorytm, to opcjonalna dyskretyzacja:
if (N > 0)
chromosom = discretMatrix(chromosom, N);
end;
po której następuje konwersja wektora na kod quasi-DNA
dna = convertToDNA(chromosom);
Wykres 6.3 przedstawia chromosom, przed oraz po konwersji na quasi-DNA.
Rysunek 6.3: Wykres ilustrujący konwersje na quasi-DNA
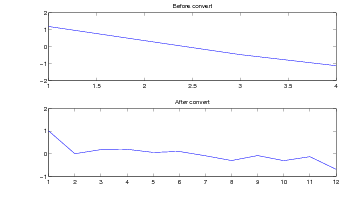
Źródło: Badania własne
Jak wiemy, kod DNA jest kodem trójkowym, tak więc konwersja polegała na losowym podziale każdego "kodonu" na 3 liczby, których suma jest równa wartości "kodonu".
Po tej operacji, możemy przeprowadzić proces krzyżowania chromosomów. W matlabie realizuje się to za pomocą następującej funkcji:
[dna1 dna2 ilecross] = crossOver(dna,convertToDNA(ch),pcross);
Tabela 6.3 przedstawia wyjściowe wektory dna1 oraz dna2 po operacji crossing-over.
Tablica 6.3: Wektory dna1 oraz dna2 po crossing-over
| L.p. | DNA1 | DNA2 |
| 1 | 0,291366416 | 0,627737516 |
| 2 | 0,116878266 | 0,690813990 |
| 3 | 0,211059595 | 0,425404461 |
| 4 | 0,120026897 | 0,112258976 |
| 5 | 0,017489069 | 0,192711298 |
| 6 | 0,056957725 | 0,298373929 |
| 7 | -0,445365159 | -0,319008968 |
| 8 | -0,043381937 | -0,022400182 |
| 9 | -0,038909092 | -0,118938851 |
| 10 | -0,236013391 | -0,422107698 |
| 11 | -0,160681180 | -0,138965678 |
| 12 | -0,735960931 | -0,495465072 |
Źródło: Badania własne
Następnym krokiem jest wykonanie ewentualnej mutacji na obu chromosomach.
% Mutowanie
[dna1 mut1] = mutacja(dna1, p_mutacji, r_mutacji);
[dna2 mut2] = mutacja(dna2, p_mutacji, r_mutacji);
Na koniec musimy zdekodować chromosomy zapisane w kodzie DNA,
% Dekodowanie DNA
chromosom1 = decodeDNA(dna1);
chromosom2 = decodeDNA(dna2);
oraz sprawdzić, który chromosom ma najwyższą korelację z wektorem ch. Jeśli oba chromosomy mają korelację większą od progowej, zostają wówczas dodane do macierzy wyjściowej DNA (tabela 6.4 ).
% Szukanie najbardziej podobnych chromosomów
% (funkcja przystosowania)
corel1 = korelacja(ch, chromosom1);
corel2 = korelacja(ch, chromosom2);
if (corel1 > min_corel && corel2 > min_corel)
out = [out; chromosom1; chromosom2];
elseif (corel1 > corel2)
out = [out; chromosom1];
else
out = [out; chromosom2];
end;
Tablica 6.4: Macierz wyjściowa po pierwszej iteracji
| L.p. | P1 | P2 | P3 | P4 |
| 1 | 0,619304276 | 0,194473691 | -0,527656188 | -1,132655502 |
| 2 | 1,743955966 | 0,603344203 | -0,460348000 | -1,056538447 |
Źródło: Badania własne
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.