
Przykładowa realizacja klasyfikacji algorytmem aiNet
Opis i znaczenie parametrów
Przykład przeprowadzono dla jednej iteracji algorytmu. Dane pochodzą z [1]. Dane zawarte w tabeli 5.1 zostały użyte jako dane wejściowe dla algorytmu Sztucznego Systemu Immunologicznego.
Parametry wykorzystane w procesie uczenia algorytmu aiNet w przykładzie:
- input - dane pobrane z tabeli 5.1
- ts = 0.05
- n = 4
- N = 10
- gen = 1
- qi = 0.2
- tp = 0.5
Poszczególne parametry mają następujące znaczenia:
- ts
- - próg supresji. Zmieniając wartość progu supresji, wpływamy na plastyczność systemu. Wszystkie przeciwciała, których metryka odległości do antygenu jest mniejsza niż wartość progu supresji, będą usuwane. Jeśli próg supresji będzie bardzo mały, wówczas algorytm nie będzie generalizował danych, tylko je zapamiętywał (uczenie pamięciowe algorytmu),
- n
- - liczba najlepiej dopasowanych przeciwciał, które będą uczestniczyć w klonowaniu,
- N
- - początkowy rozmiar pamięci globalnej M,
- qi
- - procentowa wartość klonów, które mają być ponownie wybrane,
- tp
- - próg naturalnej śmierci komórek. Jest to próg, który określa odległość, jaką muszą spełniać przeciwciała, aby naturalnie umrzeć.
Według autora niniejszej pracy, najważniejszymi parametrami algorytmu aiNet, są progi supresji i naturalnej śmierci komórek. Należy zauważyć, że zachodzi następujące równanie
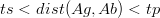 | (7.5) |
co oznacza, że wszystkie przeciwciała dodawane do wyjściowej pamięci klonalnej, posiadają wartość metryki, większą od progu supresji, ale zarazem mniejszą od progu naturalnej śmierci. Odpowiednie wyważenie tych dwóch współczynników progowych, pozwala na stworzenie dopasowanego do naszych potrzeb systemu klasyfikacyjnego.
Realizacja
Wywołanie funkcji ainet_6 w środowisku Matlab.
[M,D] = ainet6(input,ts,n,N,gen,qi,tp);
W funkcji ainet6, występuje losowy podział zbioru VAg na dwa zbiory:
- zbiór antygenów Ag - antygen (tabela 7.1 ),
- zbiór przeciwciał Ab - antybody (tabela 7.2 ).
Zbiory te dzielone są na dwie równe części, taki podział nazwany został w pracy "szczepieniem systemu immunologicznego". Pozwala to na szybsze uformowanie optymalnego zbioru przeciwciał, ale równocześnie może prowadzić do pamięciowego nauczania algorytmu.
Tablica 7.1: Zbiór antygenów
| L.p. | P1 | P2 | P3 | P4 |
| 1 | 1,0 | 0,714285714 | 0,261904762 | 0,0 |
| 2 | 1,0 | 0,155555556 | 0,777777778 | 0,0 |
| 3 | 1,0 | 0,255319149 | 0,787234043 | 0,0 |
| 4 | 1,0 | 0,729166667 | 0,250000000 | 0,0 |
| 5 | 1,0 | 0,129629630 | 0,703703704 | 0,0 |
| 6 | 1,0 | 0,055555556 | 0,851851852 | 0,0 |
| 7 | 1,0 | 0,270833333 | 0,750000000 | 0,0 |
| 8 | 1,0 | 0,250000000 | 0,750000000 | 0,0 |
| 9 | 1,0 | 0,148936170 | 0,638297872 | 0,0 |
| 10 | 1,0 | 0,708333333 | 0,250000000 | 0,0 |
| 11 | 1,0 | 0,135135135 | 0,810810811 | 0,0 |
| 12 | 1,0 | 0,625000000 | 0,208333333 | 0,0 |
| 13 | 1,0 | 0,173913043 | 0,608695652 | 0,0 |
| 14 | 1,0 | 0,608695652 | 0,260869565 | 0,0 |
| 15 | 1,0 | 0,238095238 | 0,642857143 | 0,0 |
| 16 | 1,0 | 0,340425532 | 0,680851064 | 0,0 |
| 17 | 1,0 | 0,409090909 | 0,659090909 | 0,0 |
| 18 | 1,0 | 0,311111111 | 0,666666667 | 0,0 |
| 19 | 1,0 | 0,325581395 | 0,674418605 | 0,0 |
| 20 | 1,0 | 0,163636364 | 0,818181818 | 0,0 |
Źródło: Badania własne
Tablica 7.2: Zbiór przeciwciał
| L.p. | P1 | P2 | P3 | P4 |
| 1 | 1,0 | 0,256410256 | 0,820512821 | 0,0 |
| 2 | 1,0 | 0,163636364 | 0,763636364 | 0,0 |
| 3 | 1,0 | 0,208333333 | 0,687500000 | 0,0 |
| 4 | 1,0 | 0,617021277 | 0,276595745 | 0,0 |
| 5 | 1,0 | 0,304347826 | 0,608695652 | 0,0 |
| 6 | 1,0 | 0,285714286 | 0,642857143 | 0,0 |
| 7 | 1,0 | 0,659090909 | 0,295454545 | 0,0 |
| 8 | 1,0 | 0,282608696 | 0,804347826 | 0,0 |
| 9 | 1,0 | 0,162790698 | 0,744186047 | 0,0 |
| 10 | 1,0 | 0,702127660 | 0,234042553 | 0,0 |
| 11 | 1,0 | 0,720930233 | 0,255813953 | 0,0 |
| 12 | 1,0 | 0,177777778 | 0,755555556 | 0,0 |
| 13 | 1,0 | 0,250000000 | 0,625000000 | 0,0 |
| 14 | 1,0 | 0,142857143 | 0,809523810 | 0,0 |
| 15 | 1,0 | 0,700000000 | 0,260000000 | 0,0 |
| 16 | 1,0 | 0,395348837 | 0,651162791 | 0,0 |
| 17 | 1,0 | 0,244444444 | 0,844444444 | 0,0 |
| 18 | 1,0 | 0,625000000 | 0,291666667 | 0,0 |
| 19 | 1,0 | 0,700000000 | 0,180000000 | 0,0 |
| 20 | 1,0 | 0,690476190 | 0,238095238 | 0,0 |
Źródło: Badania własne
Następnym krokiem realizowanym przez algorytm jest utworzenie macierzy odległości D, dla wszystkich przeciwciał z Ab i antygenów z Ag. Celem tej operacji jest wyznaczenie powinowactwa pomiędzy przeciwciałami a antygenami.
D = dist(Ab,Ag(vet(i), :)˘);
Dla tego przykładu wybrano odległość Euklidesową, która jest najpopularniejsza w tego typu przypadkach. Pomiędzy pierwszym antygenem (Ag1) a całą macierzą przeciwciał (Abi) obliczono za pomocą wzoru 7.2 wektor wyjściowy (tabela 7.3 ).
Najmniejsza odległość występuje pomiędzy Ag1 i Ab13, co oznacza największe powinowactwo.
Kolejnym krokiem algorytmu jest utworzenie zbioru Abm, który będzie zawierał n przeciwciał o najwyższej wartości powinowactwa.
[Dn,I] = sort(normLiniowa(D˘,zakresOd,zakresDo)˘);
Nc = floor(N - Dn(1 : n, :) * N);
Otrzymano posortowany i znormalizowany do zakresu [-1, 1] wektor odległości Dn (tabela 7.3 ).
Tablica 7.3: Wektory D, Dn oraz I
| L.p. | Wektor odległości D | Wektor odległości Dn | Wektor I |
| 1 | 0,178597256 | -1,000000000 | 13 |
| 2 | 0,141886378 | -0,917281445 | 6 |
| 3 | 0,053654037 | -0,898196790 | 3 |
| 4 | 0,527003183 | -0,832144117 | 5 |
| 5 | 0,074541350 | -0,668633357 | 9 |
| 6 | 0,047619048 | -0,663644654 | 12 |
| 7 | 0,545825906 | -0,619176607 | 2 |
| 8 | 0,167513249 | -0,569887169 | 16 |
| 9 | 0,126247061 | -0,538135864 | 8 |
| 10 | 0,618429832 | -0,503084527 | 1 |
| 11 | 0,618815047 | -0,460831746 | 14 |
| 12 | 0,127824600 | -0,430066194 | 17 |
| 13 | 0,021461615 | 0,584523025 | 18 |
| 14 | 0,191958518 | 0,598691588 | 4 |
| 15 | 0,599946332 | 0,658215337 | 7 |
| 16 | 0,157472786 | 0,829362231 | 15 |
| 17 | 0,201687264 | 0,851750931 | 20 |
| 18 | 0,522522770 | 0,887813243 | 10 |
| 19 | 0,653905761 | 0,889031422 | 11 |
| 20 | 0,607026133 | 1,000000000 | 19 |
Źródło: Badania własne
Wektor I zawiera indeksy elementów wektora D w początku od najmniejszej do największej odległości (tabela 7.3 ).
Wektor Nc zawiera liczby które określają liczbę klonów dla danego przeciwciała Ab.
Tablica 7.4: Wektor Nc
| 20 | 19 | 18 | 18 |
Źródło: Badania własne
Tabela 7.4 przedstawia wektor Nc w naszym przypadku. Jak widzimy, pierwsze przeciwciało mające największe powinowactwo otrzyma przydział na 20 klonów, drugie będzie miało 19 itd.
Po tym wszystkim, następuje proces klonowania przeciwciał.
[C,Cag,Cmi] = clone(Ab,Ag(vet(i), :),mi,D,I,Nc);
Funkcja clone zwraca zbiory: C,Cag,Cmi. Macierz C zawiera 20 klonów przeciwciała Ab13, 19 klonów przeciwciała Ab6, oraz 18 klonów przeciwciał Ab3 i Ab5. Kolejność przeciwciał ustalana jest przez wektor I, a ilość klonów przez wektor Nc.
Elementy zbioru C poddawane są mutacji w wyniku której generowany jest zbiór C˘. Według algorytmu aiNet, prawdopodobieństwo mutacji jest odwrotnie proporcjonalne do powinowactwa przeciwciał rodzicielskich z j-tym antygenem Agj tak więc, czym większe powinowactwo tym mniejsze występuje prawdopodobieństwo mutacji przeciwciała.
Kolejnym krokiem jest ponowne wyznaczenie powinowactwa pomiędzy antygenem, a zmutowanymi klonami. Poniżej przedstawiony jest kod wyznaczania powinowactwa w środowisku Matlab:
D = metrykaskalar(C,Ag(vet(i), :));
D jest wektorem odległości pomiędzy C˘ a j-tym antygenem.
Po obliczeniu miary odległości następuje sortowanie wektora D od najmniejszej do największej wartości metryki, oraz wybranie qi% najlepiej dopasowanych przeciwciał, które będą dodane do pamięci immunologicznej
[Dn,I] = sort(D);
nR = round(qi * size(C, 1));
m = C(I(1 : nR), :);
D = D(I(1 : nR));
Z powstałej macierzy m, musimy usunąć przeciwciała które mają zbyt małe podobieństwo do antygenu, jest to tzw. przycinanie sieci (Network pruning). Każdy limfocyt dla którego zachodzi równanie metryka > tp jest usuwany.
Ip = find(D > tp);
m = extract(m,Ip);
D = extract(D,Ip);
W naszym wypadku wektor Ip jest pusty tak więc nie ma komórek, których wartość metryki odległości była zbyt duża.
Tablica 7.5: Globalna pamięć immunologiczna
| L.p. | P1 | P2 | P3 | P4 |
| 1 | 1,0 | 0,123533923 | 0,811894405 | 0,0 |
| 2 | 1,0 | 0,288369657 | 0,645711665 | 0,0 |
| 3 | 1,0 | 0,196108241 | 0,754483428 | 0,0 |
| 4 | 1,0 | 0,678857896 | 0,187775582 | 0,0 |
| 5 | 1,0 | 0,617082600 | 0,265811922 | 0,0 |
| 6 | 1,0 | 0,213095731 | 0,626626421 | 0,0 |
| 7 | 1,0 | 0,171089293 | 0,700408243 | 0,0 |
| 8 | 1,0 | 0,256288660 | 0,817446133 | 0,0 |
| 9 | 1,0 | 0,721008711 | 0,255686299 | 0,0 |
| 10 | 1,0 | 0,395430193 | 0,651617606 | 0,0 |
Źródło: Badania własne
Następnym krokiem algorytmu jest zbadanie macierzy m czy nie posiada "zdublowanych" przeciwciał. Obliczone zostanie powinowactwo pomiędzy wszystkimi przeciwciałami w macierzy m, a następnie zostaną usunięte te limfocyty, które są do siebie bardzo podobne, równocześnie zostawiając jednego reprezentanta swojej klasy. Procedura ta nazywana jest supresją.
m = suppress(m,ts);
Po tym wszystkim pamięć klonalna powstała w tej iteracji, zostaje dodana do globalnej pamięci immunologicznej.
Po wykonaniu wszystkich wewnętrznych iteracji, globalna pamięć immunologiczna ma rozmiar 10x4 i przedstawiona jest w tabeli 7.5 .
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.