www.eprace.edu.pl » sztuczna-inteligencja » Znaczenie poprawnej normalizacji danych » Funkcje normalizacji

Funkcje normalizacji

Normalizacja min-max

Normalizacja min-max jest chyba najczęściej stosowanym sposobem na ujednolicenie danych wejściowych. Jest to bardzo prosta funkcja zapisywana wzorem 3.1 .
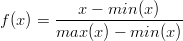(3.1)

Celem denormalizacji zbioru danych, należy odwrócić kolejność wykonywanych działań [wzór 3.2 ].
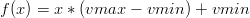(3.2)

Stałe vmin i vmax, są to wartości funkcji min() oraz max() dla zbioru x, przed procesem normalizacji. Celem denormalizacji danych, należy zachować te wartości.

Normalizacja funkcją liniową

Algorytm 3.1 , realizuje normalizację danych funkcją liniową. Dzięki takiej niecodziennej normalizacji, możliwe jest dynamiczne normalizowanie danych wejściowych do zadanego zakresu. W tradycyjnej normalizacji min-max, standardowo jesteśmy ograniczeni do przedziału [0, 1]. Normalizacja funkcją liniową omija ten problem, przez skalowanie do odpowiedniego przedziału za pomocą funkcji f(x) = ax + b zbioru wejściowego.

  1. "Mi i = 1,...,n wykonaj 2.
  2. "V Î Mi wykonaj 3.


  3. a =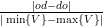

    b = do - a max{V }

    wykonaj 4.
  4. zwróć odpj = aV j + b j = 1,...,m

Opis zmiennych:

n

maksymalna ilość wektorów w macierzy

m

maksymalna ilość komórek wektora

od,do

współczynniki określające zakres normalizacji, np. [-1, 1]



Algorytm 3.1: Funkcja liniowej normalizacji danych

komentarze

Copyright © 2008-2010 EPrace oraz autorzy prac.