
Standaryzacja
Standaryzacja jest jedną z metod normalizacji danych. Różni się od normalizacji tym, że dane ustandaryzowane nie są danymi z zakresu [x; y].
Standaryzacja działa poprzez obliczenie różnicy pomiędzy daną wartością wektora i średnią wartością wektora, oraz przeskalowanie tej różnicy przez odchylenie standardowe wektora wejściowego (wzór 3.3 ).
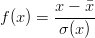 | (3.3) |
Rysunek 3.1 przedstawia histogram przykładowego wektora, który został ustandaryzowany.
Rysunek 3.1: Histogram ustandaryzowanych danych
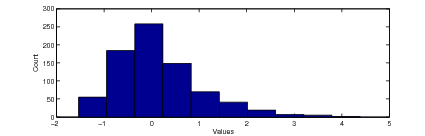
Źródło: Badania własne
Celem powrócenia do stanu przed standaryzacją, należy dane destandaryzować. Dokonuje się tego, przez odwrócenie operacji realizowanych w procesie standaryzacji. Algorytm przedstawia sposób powrotu danych, do pierwotnych wartości.
- vavg - wartość średnia wektora v przed ustandaryzowaniem
- vstd - wartość odchylenia standardowego wektora v przed ustandaryzowaniem
Gdy mamy wartości vavg oraz vstd, możemy odwrócić standaryzację, korzystając z następującego wzoru:
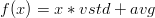 | (3.4) |
Algorytm 3.2: Destandaryzacja danych
Dla danych, które są zbliżone do średniej arytmetycznej z wektora wejściowego, wartość ustandaryzowana będzie wynosić 0, lub będzie do tej wartości bardzo zbliżona. Dzięki standaryzacji, można rozpoznawać tzw. "punkty oddalone", czyli dane, które są normalnie niespotykane lub niepoprawne.
Należy wspomnieć, że ważnymi aksjomatami standaryzacji są następujące własności:
- Średnia arytmetyczna ustandaryzowanych danych, wynosi zawsze 0
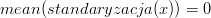
(3.5) - Odchylenie standardowe ustandaryzowanych danych, wynosi zawsze 1
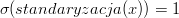
(3.6) - Wartość zbioru danych po standaryzacji należy z reguły do przedziału od -4 do 4.
Tak więc, najprostszy sposób sprawdzenia czy dane są ustandaryzowane oraz czy standaryzacja była przeprowadzona poprawnie, to sprawdzenie czy aksjomaty 3.5 , 3.6 są dla danego zbioru danych prawdziwe.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.